Biểu thức đại số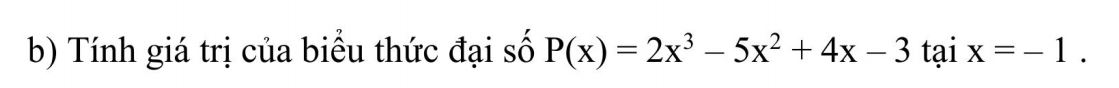
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`P=3x^2-3x^4+1/2x^5+0,75`
`=1/2x^5-3x^4+3x^2+0,75`
Bậc của B chính là bậc của hạng tử có bậc cao nhất là `1/2x^5` có bậc 5
`=>P` có bậc 5`

Ta có: \(\left(3x-\dfrac{1}{6}\right)^2>=0\forall x\)
\(\left|2y-6\right|>=0\forall y\)
Do đó: \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|>=0\forall x,y\)
mà \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|< =0\)
nên \(\left\{{}\begin{matrix}3x-\dfrac{1}{6}=0\\2y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{1}{6}\\2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{18}\\y=3\end{matrix}\right.\)

Ta có: AB=AC
=>A nằm trên đường trung trực của BC
=>AG là đường trung trực của BC
=>AG cắt BC tại trung điểm H của BC
Xét ΔABC có
AH,BD là các đường trung tuyến
AH cắt BD tại G
Do đó: G là trọng tâm của ΔABC


ta có : 25\(-y^2=8(\)\(x-2014)^2\)
\(8(x-2014)^2\ge0với\forall x\)
\(=>25-y^2\ge0\)
Mà x; y là số tự nhiên nên: \(25-8(x-2014)^2=y^2\)
\(=>y^2\le25\) và là số chính phương
\(=>y^2\in\) {0;1;4;9;16;25}
* TH1: \(y^2=\) 0
\(=\) > \(25-8(x-2014)^2=0\)
\(8(x-2014)^2=25\)
\((x-2014)^2=\frac{25}{8}\)\((loạivìx\in N)\)
các trường hợp sau làm tương tự đến khi tìm được x là số tự nhiên, sau đó suy ra y
nhớ tick nha.

Để giải bài toán này, ta sẽ thực hiện theo các bước sau:
- Tính góc A:
- Trong tam giác ABC, ta có: \(\angle A + \angle B + \angle C = 18 0^{\circ}\)
- \(\angle A + 4 5^{\circ} + 12 0^{\circ} = 18 0^{\circ}\)
- \(\angle A = 18 0^{\circ} - 4 5^{\circ} - 12 0^{\circ} = 1 5^{\circ}\)
- Xác định các đoạn thẳng:
- Cho \(C B = x\), thì \(C D = 2 x\)
- Suy ra \(B D = B C + C D = x + 2 x = 3 x\)
- Sử dụng định lý sin trong tam giác ABC:
- \(\frac{A B}{sin C} = \frac{B C}{sin A}\)
- \(\frac{A B}{sin 12 0^{\circ}} = \frac{x}{sin 1 5^{\circ}}\)
- \(A B = \frac{x \cdot sin 12 0^{\circ}}{sin 1 5^{\circ}}\)
- Sử dụng định lý sin trong tam giác ABD:
- \(\frac{A B}{sin \angle A D B} = \frac{B D}{sin \angle A}\)
- \(\frac{A B}{sin \angle A D B} = \frac{3 x}{sin 1 5^{\circ}}\)
- \(sin \angle A D B = \frac{A B \cdot sin 1 5^{\circ}}{3 x}\)
- Thay \(A B\) từ bước 3 vào:
- \(sin \angle A D B = \frac{\frac{x \cdot sin 12 0^{\circ}}{sin 1 5^{\circ}} \cdot sin 1 5^{\circ}}{3 x}\)
- \(sin \angle A D B = \frac{x \cdot sin 12 0^{\circ}}{3 x}\)
- \(sin \angle A D B = \frac{sin 12 0^{\circ}}{3}\)
- \(sin \angle A D B = \frac{\sqrt{3} / 2}{3} = \frac{\sqrt{3}}{6}\)
- Tính góc ADB:
- \(\angle A D B = arcsin \left(\right. \frac{\sqrt{3}}{6} \left.\right)\)
- \(\angle A D B \approx 16.7 8^{\circ}\)
Vậy, số đo góc ADB xấp xỉ là \(16.7 8^{\circ}\).
Bài này kết quả -11 đúng không cả nhà ơi
= 2(-1) - 5.1 + 4.-1 -3 = -11
Khi x=-1 thì \(P\left(-1\right)=2\cdot\left(-1\right)^3-5\cdot\left(-1\right)^2+4\cdot\left(-1\right)-3\)
\(=2\cdot\left(-1\right)-5\cdot1-4-3\)
=-2-5-4-3
=-7-3-4
=-14